Gostaria de discorrer sobre um assunto pouco abordado em livros de Matemática Financeira assim como na internet: as séries gradientes de pagamento. Pois bem! Quando falamos em séries de pagamentos, via de regra, pensamos em pagamentos/recebimentos uniformes, em prazos regulares de tempo, conforme diagrama abaixo:
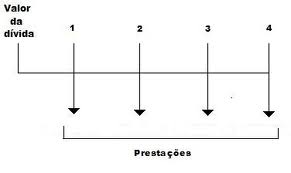
No fluxo ao lado, estamos diante de uma série postecipada de pagamentos. Nas aulas que dou, costumo enfatizar que a série postecipada será sempre nosso padrão. Ou seja, o início da série sempre vai ocorrer um período após a compra, financiamento ou assunção de dívida. As séries antecipadas e as séries diferidas, seguindo esse ponto de vista, nada mais são do que variantes da série postecipada. Os fatores relativos aos cálculos das séries uniformes postecipadas tanto do valor presente quanto do valor futuro futuro são definidos como FVA (i,n) e FAC (i,n). Facilmente encontraremos esses fatores de cálculos de séries uniformes na internet em tabelas financeiras adequadas.
O foco, contudo, deste texto não são meramente as séries uniformes e sim, como indica o título, as séries gradiente, ou séries em gradiente. Como anteriormente afirmado, a bibliografia sobre o assunto é bem difícil e esparsa. Encontrei algo interessante sobre o tema no livro de Matemática Financeira de José Dutra Vieira Sobrinho, em relação a esse tipo de séries. Também em polígrafos da disciplina de Administração Financeira dos professores universitários André Bender e Alexandre Franco, da PUC/RS e ESPM/RS, respectivamente. Não pretendo aqui teorizar/discutir/polemizar sobre o tema, mas tão-somente fazer um pequeno resumo daquilo que já estudei e já dei aulas, nesses mais de 20 anos em que ministro aulas de matemática financeira.
Antes de tudo, vamos definir o que seria uma série gradiente e quais são os modelos. A série gradiente é verificada quando temos uma série de pagamentos com algum fator G de crescimento ou decrescimento. Assim, podemos ter séries com fator de crescimento/decrescimento em progressão aritmética, conforme o exemplo do seguinte fluxo de caixa:
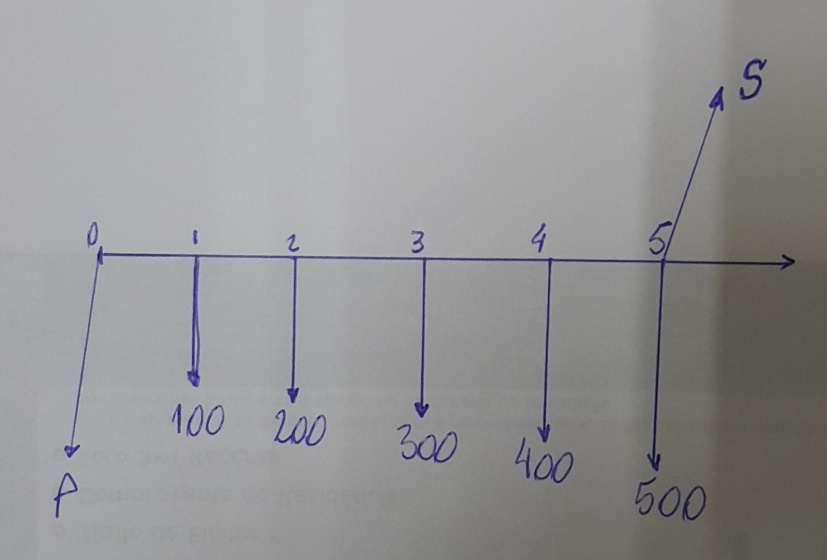Podemos ver na figura ao lado que a série começa no mês seguinte ao do financiamento, ou seja, não deixa de ser igualmente uma série postecipada. O pagamento de 100 no mês 1 segue em crescimento em progressão aritmética de razão 100 (G) até o mês 5. Notamos que a série é uma série finita, terminando no mês 5. Essa série passa a ser classificada como uma série gradiente crescente em progressão aritmética, com G=100.
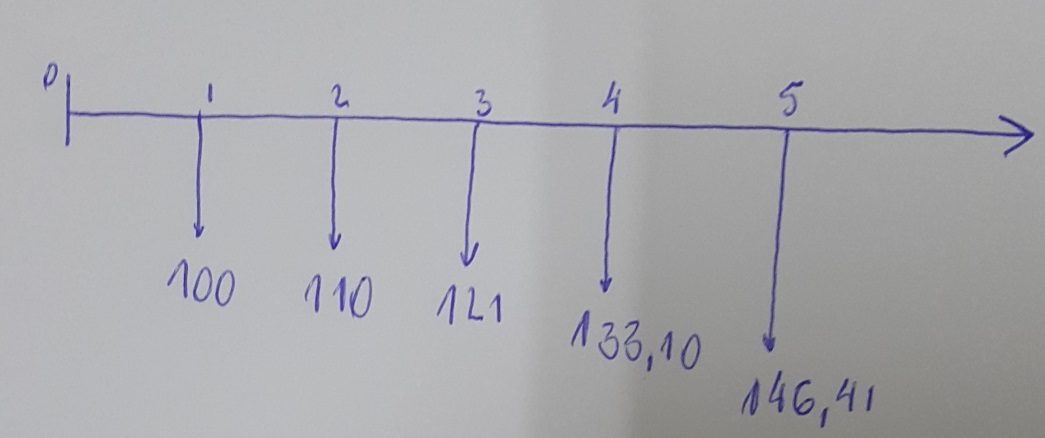Podemos ter também um série gradiente com crescimento em progressão geométrica ou crescimento exponencial, conforme a figura ao lado. Igualmente notamos que a série é postecipada, já que começa com seu primeiro pagamento no mês 1, no valor de 100. Já o segundo pagamento tem um crescimento de 10% em relação ao pagamento anterior, e assim sucessivamente. Temos, portanto, um G = 0,10, que identifica a série como gradiente em PG.
No próximo artigo pretendo continuar o tema, seguindo basicamente os dois modelos acima, séries gradiente em PA e em PG, com suas fórmulas, métodos de cálculo, e identificação dos fatores-chave pra resolver a expressão contida nas fórmulas.