E aeeee concurseiros de plantão!!!
Galera que estuda direto pra concurso de fiscal ou coisa parecida! Decidi eu, por minha conta e risco, resolver aqui, em primeiríssima mão, toda a prova de Matemática para o cargo de Técnico Tributário da Receita Estadual do Rio Grande do Sul, ou TTRE. Concurso disputadíssimo!!! Esse certame também não deixa de ser uma prévia para a prova de Auditor Fiscal da Receita Estadual (AFRE/RS). Quem quiser baixar as provas completas, acessa aqui: Bloco 1 e Bloco 2.
Buenas! Adianto que a prova foi, de certa forma, punk. Não pela dificuldade das questões, mas pelo tempo demandado por elas em razão dos cálculos manuais. Essa prova foi certamente mais complicada que a feita para Auditor da CAGE em abril de 2014. Naquela, o examinador ainda pegou leve, metendo umas questões teóricas. É aquela história… enquanto os concurseiros vão pegando malandragem de prova, o examinador vai pegando cancha de concurso…
Chega de lero-lero! Vamos à prova, começando pelas questões 25 e 26, resolvidinhas:
QUESTÃO 25 – Dado os conjuntos A = {x ϵ Z*|-1 < x ≤ 7}, B = { x ϵ N |x ≤ 4 } e C = { x ϵ Z+ | x ≤ 2 }, afirma-se que
I. (A – B) ∩ (B U C) = ø.
II. (B – A) ∩ C é um conjunto unitário.
III. (C – A) ∩ C é um subconjunto de B.
Quais estão corretas?
A) Apenas I.
B) Apenas II.
C) Apenas I e III.
D) Apenas II e III.
E) I, II e III.
Resolução: Essa é para abrir os trabalhos. Questão simples de conjuntos numéricos. O examinador tão-só exige conhecimentos de alguns conceitos, tais como de números inteiros, naturais, asterisco… além de ver se o concursando sabe operar esses conjuntos, pela subtração, união, intersecção… Vamos lá:
Eis os conjuntos:
A = {1, 2, 3, 4, 5, 6, 7}, lembrando que Z* é o conjunto dos números inteiros sem o zero.
B = {0, 1, 2, 3, 4}, esse é famoso, um N estiloso é o conjunto dos Números Naturais.
C = {0, 1, 2}, Z+ é o conjunto dos inteiros positivos, igual ao conjunto dos Naturais.
Agora, vamos fazer algumas operações entre os conjuntos:
A – B = {5, 6, 7}, elimina todos os elementos do conjunto B que estão no conjunto A.
B U C = B = {0, 1, 2, 3, 4}, como o conjunto C faz parte de B, B U C, é o próprio conjunto B.
B – A = {0}, elimina todos os elementos do conjunto A que estão no conjunto B.
C – A = {0}, elimina todos os elementos do conjunto A que estão no conjunto C.
Pronto! Agora vamos analisar cada um dos três itens:
I. (A – B) ∩ (B U C) = ø.
Tá pedindo a intersecção, ou seja, o que tem de comum entre (A – B) e (B U C). Tá procurando ainda??? Não tem nada de comum! Por isso é um zero com um risco no meio, ou , simplesmente, conjunto vazio. ITEM CORRETO.
II. (B – A) ∩ C é um conjunto unitário.
Vamos ver o que tem em comum entre (B – A) e C. A gente sempre faz isso quando olha um U virado pra baixo. Isso mesmo: U virado pra baixo significa uma intersecção, algo em comum entre duas coisas. Quando um casal de namorados tem algo em comum, eles têm uma intersecção, ok? Apenas o zero é comum a ambos, portanto estamos diante de um conjunto com apenas um elemento, ou simplesmente conjunto unitário, falou? ITEM CORRETO.
III. (C – A) ∩ C é um subconjunto de B. Estamos diante novamente do zero, que é elemento comum entre (C – A) e C. E o zero também é um elemento de B, ou seja, um subconjunto de B. ITEM CORRETO. Gabarito E.
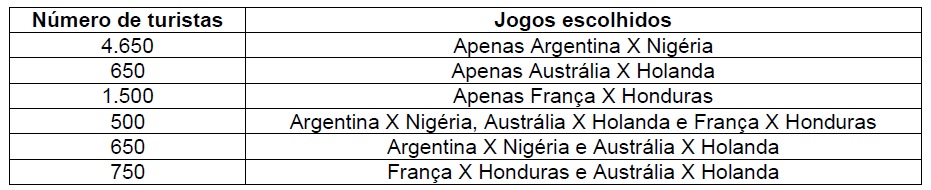
QUESTÃO 26 – Uma empresa de turismo vendeu pacotes de viagem a 7.900 turistas, que optaram por assistir a alguns dos jogos da Copa do Mundo de 2014, em Porto Alegre, na primeira fase. Esses turistas fizeram as suas opções, conforme consta no quadro abaixo:
Desses turistas, quantos optaram por assistir apenas os jogos Argentina X Nigéria e França X Honduras?
A) 150 turistas.
B) 200 turistas.
C) 250 turistas.
D) 300 turistas.
E) 350 turistas.
Resolução: Questão envolvendo conjuntos de novo. Essa fica mais fácil se montarmos rapidinho um Diagrama de Venn. Olha só como eu fiz abaixo, e escaneei pra vocês verem como ficou:
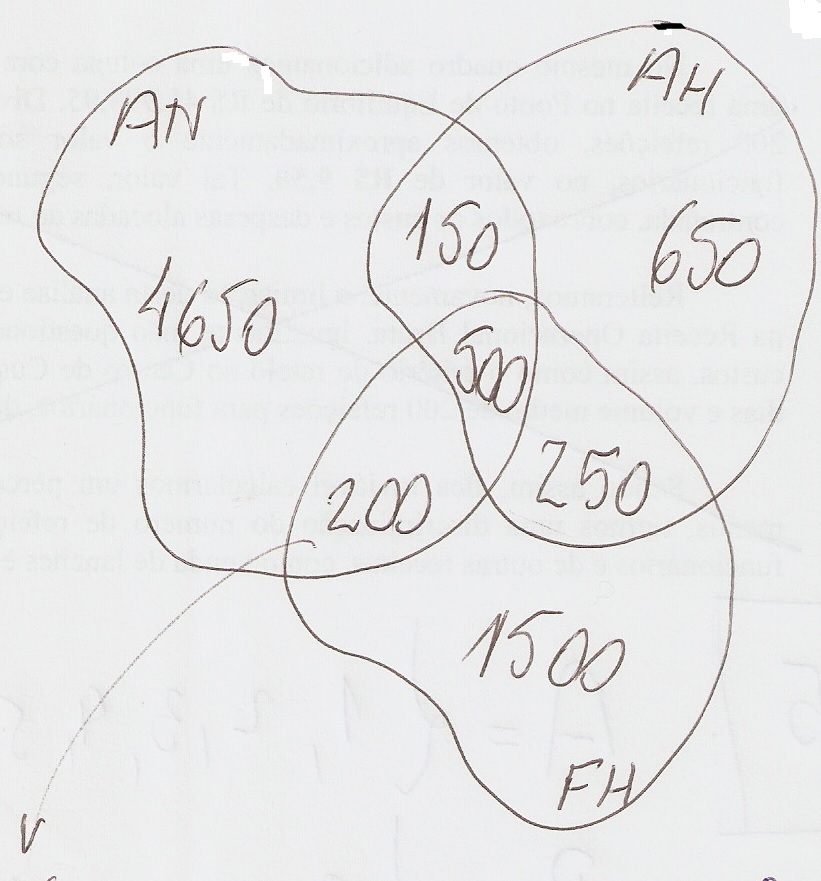Temos basicamente 3 conjuntos: pacote para o jogo de Argentina x Nigéria (AN), pacote para o jogo de França x Honduras (FH) e o pacote para o jogo de Austrália x Holanda (AH). Desenhei ao lado um círculo representando cada um desses conjuntos sobrepostos em intersecções; e vamos preenchendo cada espaço do diagrama de acordo com as informações disponíveis no quadro do comando da questão. Apenas um espaço vai ficar em branco, que é a intersecção entre FH e AN, sem participação de AH. Ora, o examinador nos dá o total de pacotes de viagem vendidos, que é 7.900. Somamos todos o valores dados no quadro (7.700) e abatemos de 7.900 = 200. Teremos a resposta de gabarito B.
No próximo post, continuo essa prova que ralou muita gente. Abraço a todos e fiquem com Deus!