Caros alunos, conforme havia prometido, vou resolvendo as questões da Fundatec de Matemática Financeira para o concurso público de Assessor Legislativo, da Câmara Municipal de Porto Alegre. Lembrando que a prova contém 15 questões: da 51 até a 56 e 58, envolvendo Matemática Financeira (é a parte que vou fazer agora); e da 57 até a 65, exceto a 58, envolvendo Estatística (que será resolvida em breve). Bom, dando uma olhada na prova de Matemática Financeira dá para dizer que a prova não foi muito fácil. Dessas 7 questões, acertando ao menos 4, já dá pra sonhar. Só precisaria de mais 3 acertos em Estatística e… ufa! continua vivo! A prova exigiu do aluno um bom domínio de álgebra e raciocínio rápido. Quem acertar as 7 questões mínimas, continua no páreo. E para quem não fez o Concurso e pretende estudar para a área fiscal, acredito que estudar esta prova será um bom treino para aferir o seu nível na matéria, afinal, Matemática Financeira e Estatística são disciplinas recorrentes em muitas provas dessa área. Também disponibilizo para download a prova completa de Assessor Legislativo, para quem quiser estudar as outras matérias ou conhecer o estilo das provas da banca Fundatec. Basta clicar que já está linkado (o arquivo está em pdf e tem aproximadamente 6 mega). Vamos então à prova!

Questão 51.

Um banco financia imóveis tanto pelo Sistema Francês (Price) quanto pelo Sistema de Amortizações Constantes (SAC). Um cliente deseja financiar um imóvel no valor de R$ 180.000,00, sem entrada, pelo prazo de 180 meses, à taxa de 1% ao mês, e achou interessante o fato de o SAC apresentar prestações decrescentes. Entretanto, as primeiras prestações pelo SAC têm valores superiores à prestação pelo Price, que, neste caso, vale R$ 2.160,30. A partir de qual parcela a prestação pelo SAC se torna menor do que a prestação pelo Price?

A) 90ª

B) 83ª

C) 77ª

D) 70ª

E) 65ª

Resposta correta: letra E. Questão de média dificuldade, o problema é que é trabalhosa e longa de fazer. Daria para fazer pelo método de tentativa e erro, analisando as alternativas. Mas também é demorado. Uma prova com média de 3 minutos por questão não dá pra ficar atravancado em uma. Eu, se fosse concursando, já pularia pra outra e deixaria para depois, se desse tempo. Então: a questão pede a partir de qual prestação o plano Price é superior ao SAC. O exercício já dá o valor da prestação pelo Price, que é de 2.160,30. Bom, sabemos que no SAC, as amortizações são constantes e iguais a 1.000, afinal, a dívida é de 180.000, devendo ser paga em 180 parcelas. A prestação é um fator resultante da soma entre juros e amortização de determinada parcela, certo? Bom, nesse caso, abatemos 1.000 de 2.160,30, e teremos 1.160,30, que seria a parcela de juros aproximada da prestação imediatamente inferior à da Price. Ocorre que os juros incidem sempre sobre o saldo devedor anterior ao da sua parcela. Ora, a taxa de juros é dada: 1%. Para termos juros de 1.160,30, o valor deve ser algo em torno de 116.000 (afnal incide 1% sobre esse valor). Abate 116.000 do total do empréstimo de 180.000 e teremos 64.000 de total amortizado. Agora, divide pelo valor da amortização por parcela (1.000), e teremos 64 parcelas. Logo, a parcela imediatamente seguinte será a 65ª – que passará a ser menor, pelo SAC, se comparada com a prestação da Price.

Questão 52.

Uma aplicação financeira no valor de R$ 10.000,00 rendeu, no regime de juros compostos, R$ 7.280,00 em três anos. Sabendo-se que a taxa de inflação no período da aplicação foi de 10% ano ano, qual a taxa real anual da operação, aproximadamente?

Utilize, caso necessário: 1,1 ao quadrado=1,210; 1,1 ao cubo = 1,331; 1,2 ao quadrado = 1,440; 1,2 ao cubo = 1,728.

A) 20%

B) 15%

C) 10%

D) 9%

E) 7%

Resposta correta: letra D. Questão mediana. Dá pra fazer rapidinho com as dicas ao final do comando da questão. Notamos que o exercício fala a respeito do rendimento de 7.280,00, ou seja, está se referindo aos juros. Assim, o montante fica em 17.280,00 (10.000 + 7.280). A fórmula básica do juro composto é essa:

Primeiro tem que encontrar o valor que capitaliza os 10.000 em 17.280. Dividimos este por aquele, e teremos 1,728. Pelo comando da questão, temos a informação de que 1,2 ao cubo = 1,728. Portanto, a taxa anual corresponde a 20%. Essa taxa é uma taxa aparente anual, pois temos de levar em conta a inflação do período em 10%, conforme informado na questão. Usando 1,2/1,1 -1 = 0,0909 = 9,09%, que será a taxa real anual da operação.

 

Questão 53.

Um banco remunera aplicações financeiras à taxa de 15% ao ano. Sabendo-se que a taxa de inflação anual é de 9%, então a a taxa real anual dessa aplicação é de, aproximadamente:

A) 6,5% positiva

B) 6,0% positiva

C) 5,5% positiva

D) 6,0% negativa

E) 6,5% negativa

Resposta correta: letra C. Primeira questão fácil e rápida. Conhecendo a matéria, dá pra fazer em menos de 2 minutos. Basta saber a fórmula de juros compostos relativa à taxa real, aparente, e com inflação: (1+A) = (1+R) x (1 + I). A remuneração nominal (aparente) do banco é de 15%, portanto o fator fica em 1,15. A inflação do período foi de 9%, assim, o fator é de 1,09. Agora ficou fácil: usando a fórmula, basta dividirmos os fatores 1,15 por 1,09; e obtemos a taxa real, que será aproximadamente de 5,5%.

Questão 54.

Uma escola tem 1.000 alunos, dos quais 66% estão no nível fundamental, e os demais estão no nível médio. Sabendo-se que 90% dos meninos e 10% das meninas estão no nível fundamental, a quantidade de meninos que está no nível fundamental é igual a:

A) 300

B) 330

C) 630

D) 660

E) 700

Resposta correta: letra C. Essa questão definitivamente não é de Matemática Financeira, pois envolve somente raciocínio lógico e uso de percentagens e de sistemas de duas equações e duas variáveis. É uma questão, no meu entendimento, de nível mediano. Vamos lá: o total de alunos no nível fundamental corresponde a 660. A soma do total de alunos (X) com alunas (Y) na escola corresponde a 1.000. Não sabemos exatamente o número de alunos e alunas que estão no nível fundamental, mas sabemos que 90% do total dos alunos, e 10% do total das alunas, estão no NF. Sabemos que esse total de alunos e alunos do NF é de 660. Pronto, está montado o nosso sistema de duas equações e duas variáveis, que podemos resolver por adição ou substituição:

X + Y = 1.000

0,90 X + 0,10 Y = 660;

Resolvendo o sistema acima, teremos o valor de X (total de meninos na escola) = 700. Dá até vontade de marcar letra E, e mandar ver a outra questão. Ocorre que essa NÂO é a resposta. O comando da questão pede o número de alunos no NF. Ora, desses 700 alunos, 90% deles são alunos do NF, portanto 700 x 90% = 630 alunos, e por consequência, 30 alunas mulheres, totalizando, assim, os 660 alunos do NF.

Questão 55.

José recebeu certa quantia em uma indenização e a aplicou em dois bancos. No primeiro, aplicou 40% da quantia total, a juros simples e à taxa de 2,5% ao mês. No segundo banco, aplicou o restante da quantia a juros simples, à taxa de 34% ao ano. Sabendo-se que o prazo de ambas as aplicações foi de 18 meses, e que José obteve R$ 29.160,00 de juros no total, pode-se afirmar que a quantia investida no segundo banco

A) é inferior a R$ 31.200,00.

B) está entre R$ 31.200,00 e R$ 32.900,00.

C) está entre R$ 32.900,00 e R$ 34.600,00.

D) está entre R$ 34.600,00 e R$ 36.300,00.

E) é superior a R$ 36.300,00.

Resposta correta: letra D. Primeira questão de juros simples na prova. Acho que é uma questão mediana, mas tem que usar álgebra pra chegar na resposta correta. Temos, primeiramente, que calcular os juros simples em função de um determinado capital que não conhecemos, particionado em dois: 0,40 C e 0,60 C. Lembrando que a segunda aplicação nos dá uma taxa anual, e teremos necessariamente de tranformá-la para mensal. Como as taxas são proporcionais, afinal, estamos no regime linear dos juros simples, a taxa mensal ficaria em 34%/12 = 2,8333% ao mês. Então, teremos:

J1 =  0,40 C x 0,025 x 18; e J2 = 0,60 C x 0,0283333 x 18; resolvendo, temos: J1 = 0,18 C, e J2 = 0,306 C.

Sabemos que o total de juros é de R$ 29.160,00. Então: J1 + J2 = 29.160; ou 0,18 C + 0,306 C = 29.160. Resolvendo essa equaçãozinha, teremos o total do capital aplicado nos dois bancos em R$ 60.000,00. No primeiro banco foi aplicado 40% desse valor, ou seja, 24.000. No segundo banco, foi aplicado o restante, ou 60% do total, que é 36.000. Portanto, a assertiva D satisfaz a pergunta do examinador, afinal R$ 36.000,00 está entre R$ 34.600,00 e R$ 36.300,00.

Questão 56.

Para complementar sua aposentadoria, uma pessoa deseja formar um fundo próprio que garanta retiradas mensais de R$ 5.000,00 por tempo indetermindado (renda perpétua). Se este fundo for formado em caderneta de poupança, que rende 0,5% ao mês, qual deverá ser o montante, de modo a garantir as retiradas pretendidas:

A) R$ 5.000.000,00

B) R$ 4.000.000,00

C) R$ 3.000.000,00

D) R$ 2.000.000,00

E) R$ 1.000.000,00

Resposta correta: letra E. Essa é a mais fácil de todas! Para quem estudou rendas perpétuas, sabe que foi fácil. Basta dividirmos as retiradas mensais de R$ 5.000,00 pela taxa de 0,005 (não esqueça de usar a taxa na forma unitária). Teremos o valor de R$ 1.000.000,00 (um milhão de reais). Com esse valor na conta, definitivamente ninguém passa fome. Mesmo sendo burro, e colocando o dinheiro na poupança…

Questão 58.

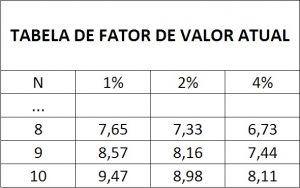
Um imóvel está à venda por dez prestações bimestrais iguais a R$ 10.000,00 cada uma, sendo que a primeira deverá ser paga como entrada. Sabendo-se que a taxa da operação é de 4% ao quadrimestre, com capitalização bimestral, qual o valor à vista deste imóvel? Utilize, caso necessário, a tabela a seguir:

A) R$ 94.700,00

B) R$ 91.600,00

C) R$ 89.800,00

D) R$ 84.400,00

E) R$ 81.100,00

Resposta correta: letra B. Mais uma questão barbada de Matemática Financeira. Essa, agora, envolve o conteúdo de séries uniformes de pagamentos. A questão versa sobre uma série de 10 pagamentos bimestrais antecipados. É-nos dado o valor das prestações uniformes de R$ 10.000,00. Antes de tudo, temos de transformar a taxa dada, pois ela está na forma nominal. Como a taxa é quadrimestral, capitalizada bimestralmente, temos de dividir o valor dela por 2, afinal, temos dois períodos bimestrais dentro de um quadrimestre, certo? Então fazemos: 4/2 = 2% ao bimestre efetivos. Pronto! Temos os períodos bimestrais, a taxa bimestral, a prestação… só falta a resposta! Bom, eu, particularmente, prefiro tratar essa série como uma série postecipada de 9 pagamentos, considerando uma entrada de R$ 10.000,00. Acho mais simples resolver assim. Então: PV = R x FVA (2%, 9) = 10.000 x 8,16 = 81.600, que é o valor presente de minha série postecipada. Agora é só somar com a entrada, que já está na data zero, e temos R$ 91.600,00 como preço à vista deste imóvel. Lembrando que esse fator de 8,16, eu peguei ali na tabela fornecida no comando da questão. Essa eu achei fácil e rápida.

Bom, creio que a primeira parte da prova, que envolvia o conteúdo de Matemática Financeira está completamente resolvida. A outra parte da prova envolve Estatística, e pretendo resolver também. Por enquanto, espero ter ajudado! Não esqueçam: estudo contínuo até ser nomeado. E abraço e bons estudos a todos!