Vamos agora resolver e comentar a segunda parte da prova de Matemática, da banca Fundatec, para o Concurso Público para provimento do Cargo de Assessor Legislativo da Cãmara Municipal de Porto Alegre, realizada em janeiro de 2012,  com questões de Estatística. Mais precisamente, 8 questões de Estatística. Também disponibilizo para download a prova completa de Assessor Legislativo, para quem quiser estudar as outras matérias ou conhecer o estilo das provas da banca Fundatec. Basta clicar que já está linkado (o arquivo está em pdf e tem aproximadamente 6 mega). Vamos à prova comentada então:

Questão 57.

Um Shopping Center possui dois sistemas automáticos de proteção contra incêndios. A eficiência de cada sistema, segundo o fabricante, é de 99%. Sabendo-se que os sistemas funcionam de modo totalmente independente e que ambos permanecem ligados 24 horas por dia, qual é a probabilidade de que um incêndio seja detectado e neutralizado?

A) 99,99%

B) 99,00%

C) 98,01%

D) 97,00%

E) 96,66%

Resposta correta: letra A. Nessa questão, devemos lembrar o conceito de eventos ou sistemas independentes. Na figura abaixo, imaginemos 3 eventos independentes. Nesse caso, percebemos que a ocorrência de um não exclui a do outro, e vice-versa. Em eventos independentes, há ocorrência simultânea, sem problemas! Na questão dada, a eficiência individual de cada um dos sistemas de proteção contra incêndios é de 99%. Ou seja, a chance de que cada um venha a falhar é de 1% (100% – 99%). Ou o sistema funciona, ou falha! Desse modo, a chance de que os dois venham a falhar será de 1% x 1%. Uma chance pequena, convenhamos. (1/100) x (1/100) = 1/10.000, que fica em 0,0001. Multiplicamos esse valor por 100, e teremos a forma percentual de que os dois sistemas falhem: 0,01%. Somente nesse caso vai dar furo no sistema de segurança do Shopping Center. Em quaisquer outras circunstâncias, o sistema detectará um possível incêndio. Então, para sabermos a probabilidade de que um incêndio seja detectado e neutralizado, basta fazermos 100% – 0,01% = 99,99%. Somente 0,01% não pode ocorrer, o resto pode!

Questão 59.

Os 156 funcionários de certa empresa têm salário médio de R$ 1.000,00, com desvio-padrão de R$ 200,00. Sabendo que houve nessa empresa um reajuste salarial de 20% e mais um abono de R$ 200,00, é correto afirmar que:

A) O coeficiente de variação do novo salário é igual a 20%.

B) O coeficiente de variação do antigo salário é igual a 17,14%.

C) O coeficiente de variação do novo salário é maior do que o coeficiente de variação do antigo salário.

D) O coeficiente de variação do novo salário é menor do que o coeficiente de variação do antigo salário.

E) O coeficiente de variação não sofreu qualquer alteração.

Resposta correta: letra D. Questão QUASE igual à uma recente elaborada pela Banca da FMP, para o Concurso Público de Auditor Público Externo do TCE. Resolvi ela um dia antes da prova com minha turma de um curso preparatório. E resolvi também dias antes aqui mesmo no site: olhem aqui. Realmente faltou criatividade para quem elaborou essa questão. Bom, a questão versa sobre propriedades da média e do desvio-padrão. Lembrando: a média aritmética é afetada por todas operações (soma, subtração, divisão e produto) que alteram cada elemento de uma distribuição. No desvio-padrão, somente a divisão e o produto dos elementos por uma constante afetam esse desvio. Lembrando que o Coeficiente de Variação é uma medida resultante da razão entre o desvio e a média, e seu resultado, se multiplicado por 100, ficará sempre entre 0% e 100%. Quanto mais próximo de 100%, mais heterogênea é a distribuição. Quanto mais próximo de 0%, mais homogênea será a distribuição. O Coeficiente de Variação antigo será de 200/1.000 = 0,20 ou 20%. Considerando, agora, a nova situação, ou seja, com um reajuste salarial de 20% e mais um abono de R$ 200,00: multiplicamos a antiga média por 1,20 e somamos com 200. Logo, a nova média salarial será de R$ 1.400,00. Como o desvio-padrão é afetado somente pela multiplicação, temos que o novo desvio-padrão será de R$ 240,00. E, portanto, o novo Coeficiente de Variação será igual a 240/1400 = 0,1714, ou em valores percentuais de 17,14%. Notamos que, com os reajustes salariais e com o abono, o coeficiente de variação passou de 20% para 17,14%. Assim, o coeficiente de variação do novo salário é menor do que o coeficiente de variação do antigo salário. Questão muito fácil!

Questão 60.

Um veículo importado custa R$ 500.000,00, e o seguro total vale R$ 30.000,00. Com base em levantamentos estatísticos, esse veículo apresenta 2% de probabilidade de sofrer algum sinistro com perda total. Desse modo, o valor líquido que uma seguradora espera ganhar em cada seguro vendido para esse tipo de veículo é igual a

A) R$ 12.500,00

B) R$ 14.800,00

C) R$ 15.500,00

D) R$ 17.800,00

E) R$ 19.400,00

Resposta correta: letra E. O valor do seguro é de R$ 30.000,00. Abatemos desse valor o percentual de 2% sobre R$ 500.000,00, que é igual a R$ 10.000,00 por veículo. Também sabemos que 20% desses R$ 30.000,00 não valem a pena, ou seja, R$ 600,00. Então 30.000 – 10.000 – 600 = 19.400. Questão fácil.

Questão 61.

Os dados abaixo se referem ao salário mensal (em R$) e à carga horária semanal (em horas) de 50 funcionários de certa empresa:

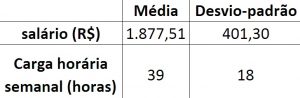A partir dos resultados obtidos, em termos relativos, assinale a alternativa cuja variável possui a menor variabilidade e a correta justificativa.

…

A) O salário, pois tem maior desvio padrão.

B) O salário, pois o coeficiente de variação é menor.

C) A carga horária, pois tem menor variação absoluta.

D) A carga horária semanal, pois o desvio padrão é menor.

E) A carga horária, pois tem menor média e desvio padrão.

Resposta correta: letra B. De cara, sem fazer contas, eu responderia letra B. Quando queremos comparar a dispersão de duas variáveis quaisquer, sejam quais forem suas medidas, o parâmetro adequado para isso é a medida relativa denominada de coeficiente de variação. A única alternativa que justifica a variabilidade menor é a letra B. Contudo, vamos aos cálculos. Para calcularmos o coeficiente de variação de determinada variável, basta fazermos a razão entre seu desvio padrão e sua média. Então, seguindo esse conceito, para o salário, dividimos 401,30/1.877,51 = 0,2137, ou 21,37% de variabilidade. Para a carga horária semanal, temos 18/39 = 0,4615, ou 46,15%. Desse modo, o salário tem uma variabilidade menor que a da carga horária, tendo, assim, uma distribuição mais homogênea. Pelas alternativas, nem precisava cálculos para resolver essa.

Questão 62.

Uma turma de Estatística de certa Universidade tem 12 alunos. Um desses alunos desistiu do curso e outro aluno, com 18 anos de idade, ocupou sua vaga. Desse modo, a média de idades dos alunos dessa turma diminuiu 18 meses. A partir desses dados, pode-se afirmar que o aluno que desistiu do curso tem

A) 24 anos

B) 30 anos

C) 36 anos

D) 40 anos

E) 44 anos

Resposta correta: letra C. Sabemos que a média da idade, em anos, dos 12 alunos é a soma de suas idades dividido por 12. Consideremos 11 alunos mais o que saiu do curso, que vou chamar de aluno X. A soma das idades dos 11 alunos que permaneceram no curso, eu vou chamar de A. E a primeira média, vou chamar de M. Então temos:

(A + X)/12 = M, ou simplesmente, A + X = 12M, ou A = 12M – X

Como o alunos X foi embora e entrou outro aluno com 18 anos e a média ficou reduzida em 18 meses, lembrando que 18 meses corresponde a 1,5 anos, temos o seguinte:

(A + 18)/12 = M – 1,5, passando o 12 para o outro lado multiplicando, temos: A +18 = 12M – 18, ou seja, A = 12M – 36.

Finalmente, igualamos as duas expressões de A: 12M – X = 12M – 36. Resolvendo, teremos X = 36. Questão de álgebra pura e raciocínio lógico. Pra mim, quem faz essa questão em 3 minutos, conhece o assunto! Dificuldade mediana.

Questão 63.

Durante 4 anos consecutivos, o cliente de uma gráfica mandou imprimir cartões de visita para sua empresa. No primeiro ano, a gráfica cobrou R$ 10,00 o cento; no segundo ano, R$ 12,00; no terceiro, R$ 15,00; e no quarto, R$ 20,00. Sabe-se que, durante o período considerado, o cliente gastou exatamente R$ 3.000,00 em cada ano. Nessas condições, o custo médio do centro de cartões para o período de 4 anos foi de, aproximadamente,

A) R$ 11,11

B) R$ 13,33

C) R$ 14,25

D) R$ 15,33

E) R$ 17,66

Resposta correta: letra B. Sabemos que em cada ano o cliente gastou exatamente R$ 3.000,00, ou seja, no período de 4 anos, o cliente gastou um total de R$ 12.000,00. Precisamos saber quantos centos o cliente mandou imprimir ao longo desse período. No primeiro ano, o cento custava R$ 10,00. Nesse ano, a empresa gastou R$ 3.000,00; logo, fazemos a divisão de 3.000/10 = 300. Teremos 300 centos impressos no primeiro ano. No segundo ano, o cento custava R$ 12,00. Nesse ano, a empresa gastou R$ 3.000,00; logo, fazemos a divisão de 3.000/12 = 250. Teremos 250 centos impressos no segundo ano. No terceiro ano, o cento custava R$ 15,00. Nesse ano, a empresa gastou R$ 3.000,00; logo, fazemos a divisão de 3.000/15 = 200. Teremos 200 centos impressos no terceiro ano. Finalmente, no quarto ano, o cento custava R$ 20,00. Nesse ano, a empresa gastou R$ 3.000,00; logo, fazemos a divisão de 3.000/20 = 150. Teremos 150 centos impressos no quarto ano. Portanto, o total de centos impressos nos 4 anos foi de 300 + 250 + 200 +150 = 900. Sabemos também que nos 4 anos, o cliente gastou um total de R$ 12.000,00. Então, fazemos uma média de 12.000/900 = 13,33. Que será o valor médio do cento ao longo desse período de 4 anos.

Questão 64.

Para o conjunto 20, 40 e 80, pode-se afirmar que:

A) A média aritmética é menor do que a média harmônica e maior do que a média geométrica.

B) A média harmônica é maior do que a média geométrica e menor do que a média aritmética.

C) A média geométrica é maior do que a média harmônica e menor do que a média aritmética.

D) A média geométrica é maior do que média aritmética e também é maior do que a média harmônica.

E) As médias harmônica, geométrica e aritmética são todas iguais.

Resposta correta: letra C. Para um rol de números positivos quaisquer teremos sempre a média aritmética superior à média geométrica, e esta superior à média hamônica. Ora, temos então importante propriedade: para quaiquer números positivos SEMPRE teremos: MA > MG > MH. Sabendo disso, ganha-se importante tempo na prova. Mas se não soubéssemos dessa propriedade, teríamos de conhecer as fórmulas dessas 3 médias: aritmética, geométrica e harmônica; e calculá-las no braço. A mais simples de calcular, sem dúvida, é a média aritmética. Basta fazermos a soma dos elementos e dividir por 3: (20 + 40 + 80) / 3 = 46,66. Na média geométrica, multiplicamos os elementos e tiramos sua raiz cúbica, ou seja: raiz cúbica de (20 x 40 x 80) = 64.000. Essa raiz cúbica não é difícil de calcular. Fica em 40, afinal, a raiz cúbica de 64 = 4, pois 4 x 4 x 4 = 64. Por fim, a média harmônica é igual a 3 dividido pela soma dos inversos de cada elemento: 3 / (1/20 + 1/40 + 1/80) = 34,28. Logo, temos MA = 46,66; MG = 40; e MH = 34,28.

Questão 65.

A tabela a seguir mostra a distribuição de salários dos funcionários de certa empresa:

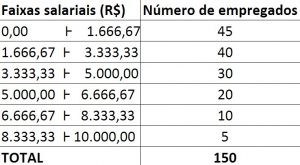A moda bruta e a porcentagem de funcionários que ganham salários entre R$ 6.666,67 e R$ 10.000,00 são, respectivamente,

 

 

A) R$ 833,33 e 10%

B) R$ 833,33 e 23,33%

C) R$ 833,33 e 35%

D) R$ 2.500,00 e 10%

E) R$ 2.500,00 e 23,33%

Resposta correta: letra A. A moda bruta é muito fácil calcular: é simplesmente o ponto médio da classe modal. A classe modal corresponde à primeira classe, pois nela temos 45, que é o maior número de ocorrências. Como se trata de uma distribuição por intervalos de classes, fazemos a média entre o limite inferior e o limite superior da classe modal. O limite inferior é zero, e o superior é 1.666,67. Somamos e dividimos por 2, que vai dar 833,33 o valor da moda bruta.

A porcentagem de funcionários que ganham salários entre R$ 6.666,67 e R$ 10.000,00 também é bem fácil de calcular. Sabemos que nessa faixa temos os dois últimos intervalos de classe, que totalizam, juntos, 15 funcionários. Então, é só fazer a relação de 15 para o total de funcionários, ou seja, 15/150 = 0,10. Ou seja, 10% dos funcionários ganham salários entre R$ 6.666,67 e R$ 10.000,00. Essa questão foi pra dar uma mãozinha pra galera.

Bom, das 15 questões que resolvi de Matemática, da prova de Assessor Legislativo da Câmara Municipal de Porto Alegre, da Banca Fundatec, não encontrei nenhuma que fosse passível de recurso. Realmente os gabaritos fornecidos apontam para as respostas corretas. Espero ter ajudado, e clareado algumas dúvidas a respeito das questões. Sei que o melhor método de estudo é resolvendo questões, por isso, sempre que possível, vou postar por aqui questões resolvidas dos mais variados concursos recentes. Quaiquer dúvidas que venham a ter, postem aqui seus comentários, que não demorarei para responder. Abraço a todos, e bons estudos!