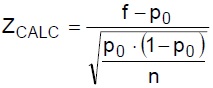Resolvo aqui questão sobre testes de hipóteses constante de concurso público realizado em 2010 pela Fundação Cesgranrio, para Analista de Pesquisa Operacional da Petrobrás. A questão envolve o conteúdo de Testes de Hipóteses para proporções.
Lembrando que, pela internet, somente aqui o estudante encontra questões de provas recentes detalhadamente resolvidas sobre conteúdos tais como: Contabilidade, Estatística, Matemática Financeira, Matemática e Pesquisa Operacional.
Vamos à questão:
Um fabricante deseja fazer um estudo, com uma confiança de 95%, a respeito da aceitação de um dos seus produtos com a finalidade de lançá-lo em um novo mercado. Esse novo lançamento somente será comercialmente viável se o índice de aceitação do produto for, pelo menos, de 90%.
Para tal, realizou uma pesquisa de mercado em uma das cidades onde seu produto já é comercializado. Foi perguntado aos consumidores se gostaram (aceitaram) do produto.
O resultado foi o seguinte:
850 consumidores responderam que gostaram do produto e 150 consumidores responderam que não gostaram do produto.
Qual será a estatística de teste a ser utilizada nesse teste?
(A) -5,27
(B) -1,96
(C) -1,65
(D) 1,96
(E) 5,27
Resolução: É informado que o lançamento do produto somente será viável se o índice de aceitação do produto for, pelo menos, de 90%. Na verdade, esse “pelo menos”, quer dizer, maior ou igual, superior, a 90%. Esse será o nosso teste, ou seja, a denominada hipótese alternativa, ou H1. Quando analisamos valores maiores para um teste, esse teste chama-se unilateral à direita, ou unicaudal à direita, conforme a figura abaixo:
Temos, assim, duas hipóteses:
– H0: é a hipótese nula, ou básica, ou seja, Π < 0,90. Π é o parâmetro da proporção populacional. Se refere à população como um todo, ou uma referência conclusiva sobre este parâmetro. Quando aceitamos Ho, nada podemos afirmar sobre o teste e, assim, acabamos por rejeitar H1, que é a hipótese do teste, ou seja, a hipótese alternativa.
– H1: é a hipótes alternativa, ou a hipótese de teste. Ao concluirmos pela aceitação de H1, e consequente rejeição de Ho, definimo-nos pela validade do teste. Nesse caso, Π >=0,90, será nosso teste alternativo.
Retomando: o teste é unilateral à direita, pois estamos avaliando valores maiores que o estipulado de 0,90. Por isso unilateral ou unicaudal. Na figura acima, a área de rejeição de Ho, ou seja, a área em verde escuro, corresponde ao nível de significância do teste, também denominado α (alfa). A questão, na verdade, nos informa o valor de Β (beta), que é o nível de confiança. Temos que α = 1 – Β. Assim, α = 1 – 0,95 = 0,05, ou simplesmente 5%. Esses 5% correspondem à área hachurada da figura acima, que equivale a 5% da área de toda a curva sob o eixo horizontal. A significância do teste também está diretamente relacionada ao erro tipo I, ou seja, a probabilidade de rejeitarmos Ho, sendo ele verdadeiro.
Definido α, precisamos encontrar o valor crítico de Z. Reitero aqui que em testes de hipóteses com proporções somente usamos a tabela normal (Z); nada de usar tabela T, certo? Considerando Z como o eixo horizontal, onde a média = moda = mediana = 0, cujo valor de zero está no centro da curva de Gauss (ou de sino), e seus valores acima da média zero são positivos e abaixo são negativos.
Voltando ao valor crítico: esse valor é tabelado. Pegamos na tabela normal o valor correspondente a uma área de 0,05 à direita. Ao vermos na referida tabela, encontramos um valor de Z correspondente a 1,65. Ou seja, esse valor de 1,65 será o nosso Z crítico, a partir do qual rejeitamos H0, ou antes do qual, aceitamos Ho. Esse vai ser o nosso valor de referência.
Próximo passo, agora, será encontrarmos o Z calculado, ou estatística de teste, que é obtido a partir da fórmula abaixo:
.
.
Onde temos:
f: corresponde à proporção amostral, calculada com os dados da questão 850/1.000 = 0,85, que seria o total de alunos que gostaram do produto, e 1.000 corresponde ao total de alunos entrevistados, ou seja, é a amostra n.
n: é o tamanho da amostra dado, ou seja, do número de entrevistados de 1.000.
P0: se refere à proporção de 90%, ou 0,90, ou simplesmente Π. Ao substiuirmos estes valores na fórmula e resolvendo, chegamos ao valor da estatística do teste, que é de – 5,27. Tal valor encontra-se à esquerda da cauda: então, nem pensar em rejeitar Ho. Tão-somente rejeitaríamos H0 com valores da estatística do teste acima de 1,65 ( Z crítico ), conforme comentei acima.
Concluímos, portanto, que não podemos rejeitar H0, a um nível de significância de 5%, isto é: não há evidências de que o percentual de aceitação do produto seja superior a 90%, não sendo viável o lançamento do produto. Na verdade, quando não rejeitamos H0, estamos simplesmente dizendo que nada podemos afirmar sobre a veracidade da hipótese alternativa.
No caso da questão, solicitava-se apenas o valor da estatística de teste e o conhecimento da fórmula para chegarmos ao seu cálculo. Naturalmente, para que conheçamos a aplicação da fórmula, devemos conhecer os fundamentos dos testes de significância. Letra A.
Não são todos os concursos que requerem esse conteúdo, mas resolvi postar algo sobre esse tema, visto que têm surgido questões de concursos para diversos cargos de nível superior que exigem alguns conhecimentos teóricos a respeito dos testes de hipóteses. Tenho notado isso de uns anos para cá.
Fico por aqui, caros amigos visitantes. Exercícios resolvidos e comentados são postados regularmente neste blog. Aquelas questões que ninguém se atreve a comentar, eu encaro: e com baixa margem de erro amostral…
Fiquem com Deus.