Vou começar a semana resolvendo a prova de Matemática do Concurso Público para Agente Fiscal da Receita Municipal de Porto Alegre, realizada ontem, domingo, dia 25/03/2012, pela Banca da Fundação do Ministério Público (FMP). Um amigo me conseguiu a prova e não me contive em resolvê-la antes mesmo de liberarem os gabaritos: gosto de correr o risco de errar… A prova contém questões envolvendo conteúdos de matemática geral e Matemática Financeira.

Acredito que somente aqui, neste site, em primeiríssima mão, a prova de Matemática está detalhadamente resolvida. Pretendo, sempre que possível, publicar novidades por aqui, especialmente dessas matérias em que sou metido a dar aulas. Fiquem ligados, e volta e meia passem por aqui…

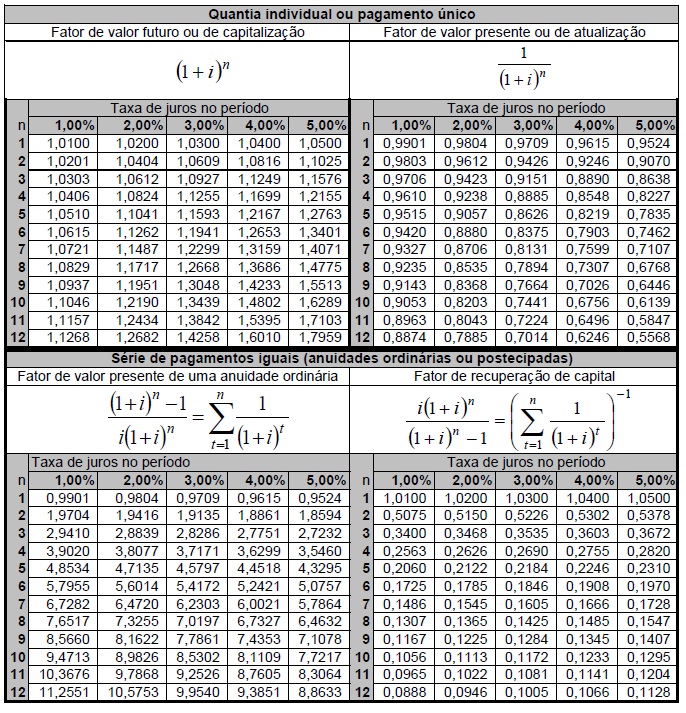
Senhores: a prova disponibilizou, como recurso de cálculo, as seguintes tabelas financeiras abaixo; aliás, essas tabelas financeiras já são figuras carimbadas da Banca da FMP:

51. O gerente de uma loja dispõe de 6 vendedores para formar equipes de vendas cada uma constituída de 3 vendedores. O número de equipes com combinações diferentes de vendedores que o gerente poderá fazer é

A) 6

B) 18

C) 20

D) 120

E) 720

Resolução: Me parceu fácil essa questão. Eu resolvi como uma combinação simples de 6 elementos tomados 3 a 3. Basta fazer (6 x 5 x 4) / 3! = 20. Lembrem-se: equipes, grupos e comissões envolvem sempre combinações. Letra C.

52. O vigésimo quinto termo da progressão (3, 10, 17, …) é

A) 182

B) 178

C) 175

D) 171

E) 168

Resolução: Depois de uma prova ralada como foi a de Estatística, esta questão de Progressão Aritmética me pareceu um bálsamo. Antes de tudo, percebemos que a razão da PA é igual a 7. Sendo positiva, é uma PA crescente. Aplicamos a fórmula abaixo:

.

.

.

Logo, o vigésimo elemento da sequência é … 3 + (25 -1) . 7 = 171. Letra D – questão para não errar.

53. Uma indústria de calçados tem melhorado a produtividade de seus processos. A cada ano consegue produzir 20% a mais de calçados em relação ao ano anterior. Sabendo-se que a produção de calçados no ano de 2011 foi de 15.000, a expectativa de produção total nos anos de 2011 a 2015 é de

A) 126.000

B) 111.624

C) 105.000

D) 90.000

E) 75.000

Resolução: Essa questão é outra que não dá para perder. Envolve Progressão Geométrica. Como a PG é pequena, dá para ir fazendo no braço… nada de fórmulas! Ficaria assim, a produção de calçados de 2011 a 2015:

15.000 + 18.000 + 21.600 + 25.920 + 31.104 = 111.624 (produção total nos 5 anos). Letra B.

54. Os lados de um triângulo medem 6 cm, 8 cm e 10 cm. A área do triângulo, em cm², é

A) 12√2

B) 15√2

C) 24

D) 30

E) 40

Resolução: Estamos diante de um triângulo retângulo pitagórico, parente do 3, 4, e 5 (multiplicado por 2). Os catetos são 6 e 8, formando, portanto, um ângulo reto entre si. Sabemos que a base e a altura formam sempre um ângulo reto.

A fórmula da área de qualquer triângulo, no qual temos a altura é:

A = (b x h) / 2 = (6 x 8) /2 = 24. Letra C.

Até aqui, dava para acertar todas!

55. Uma aplicação de R$ 4.000,00, à taxa de juros simples de 4% ao mês, após 90 dias, obteve um rendimento de

A) R$ 480,00

B) R$ 499,60

C) R$ 4.480,00

D) R$ 4.499,60

E) R$ 4.521,12

Resolução: Questão tranquila de juros simples. Está pedindo somente os juros (ou rendimentos), em 90 dias, ou 3 meses. A fórmula dos juros simples é dada por: J = C . i . n = 4.000 . 0,04 . 3 = 480,00. Estou aqui quase dormindo, mas essa eu não erro: letra A.

56. Um capital no valor de R$ 1.000,00 foi aplicado em um fundo durante 1 semestre a uma taxa de juros de 12% ano ano, capitalizados mensalmente. O montante, ao final da aplicação, foi de

A) R$ 943,40

B) R$ 942,05

C) R$ 1.058,30

D) R$ 1.060,00

E) R$ 1.061,50

Resolução: Questão de Juros Compostos. Pela taxa na forma nominal a gente percebe isso! Afinal, 12 % ao ano com capitalização mensal corresponde a 1 % ao mês, capitalizados mensalmente, em juros compostos. Temos de usar sempre a taxa na forma efetiva, nunca na nominal! Pegamos, na primeira tabela dada, o fator de capitalização para aplicação de um único valor: coluna do 1%, cruzando com a linha 6, e teremos o fator 1,0615. Agora multiplicamos esse fator pelo capital de 1.000,00, e teremos sem sombra de dúvidas a resposta da letra E. Para quem quer ser Agente Fiscal, essa questão ainda está fácil.

57. Uma loja financiou um eletrodoméstico, no valor à vista de R$ 1.200,00, em 10 prestações mensais, iguais e sucessivas, vencendo a primeira 3 meses após a compra. Sabendo-se que a taxa de juros utilizada foi de 2% ao mês, o valor da prestação é de

A) R$ 128,38

B) R$ 130,94

C) R$ 133,56

D) R$ 138,96

E) R$ 141,69

Resolução: Questão de séries uniformes de pagamentos. Temos de capitalizar esse valor de 1.200 até o mês 2, afinal, ele será o valor presente de nossa série postecipada. Esqueceram? O valor presente de qualquer série postecipada cai sempre um mês antes da primeira prestação. E, por padrão, trabalhamos sempre com séries postecipadas. Isso é básico fazer, senão, erraremos a questão. Fazendo essa capitalização, teremos o PV da série em 1.248,48.

Quando queremos saber o valor da prestação, usamos a tabela do Fator de Recuperação de Capital (FRC). Assim, vamos a essa tabela (a última fornecida). Procuramos na coluna 2, linha 10, e teremos o fator 0,1113, o qual multiplicamos pelo valor presente que acabamos de capitalizar até o mês 2.

Ou seja, 1.248,48 . 0,1113 = 138,96. Letra D. Fiz umas duas dessas em meu curso, ninguém pode reclamar, ao menos de mim…

58. Uma empresa obteve num banco o financiamento de R$ 10.000,00, pelo Sistema de Amortizações Constantes – SAC, em 10 pagamentos mensais, sucessivos, o primeiro vencendo um mês após a liberação do valor financiado. Sabendo-se que a taxa de juros utilizada pelo banco foi de 3%, o valor da segunda prestação é de

A) R$ 1.270,00

B) R$ 1.221,00

C) R$ 1.172,00

D) R$ 1.000,00

E) R$ 270,00

Resolução: No SAC, temos todas as amortizações iguais. O valor de cada amortização é obtido pela divisão do empréstimo pelo número de pagamentos. Assim, temos A = 10.000 / 10 = 1.000. Em cada amortização, teremos, portanto, o valor de R$ 1.000,00. Os juros pagos na segunda parcela incidem sobre o saldo devedor após o pagamento da primeira parcela. Após o pagamento da primeira parcela, teremos 10.000 – 1.000 = 9.000, que será nosso novo saldo devedor após pagar a primeira parcela. Sobre esse valor, incidem juros de 3%. Assim, J = 3% . 9.000 = 270. Sabemos que cada parcela, é a composição de juros mais amortização, ou seja, P = J + A = 270 + 1.000 = 1.270. Letra A.

59. A taxa aparente de juros de uma aplicação financeira foi de 16% ao ano. Sabendo-se que a taxa de inflação anual foi de 6%, a taxa real anual de juros é de

A) 2,17%

B) 9,43%

C) 10,00%

D) 22,00%

E) 22,96%

Resolução: Questão trivial envolvendo taxa real, inflação e taxa aparente (nominal). Sabemos que:

(1 + R) = (1+A) / (1 + I), assim,

(1 + R) = 1,16/1,06 = 1,0943, assim, temos que R = 1,0943 – 1 = 0,0943 . 100 = 9,43%. Letra B.

60. Uma empresa pretende investir R$ 9.000,00 e possui quatro alternativas de projetos de investimentos com duração de 3 anos. Todas as alternativas consideram o investimento projetado para o início de cada projeto e com fluxos de caixa anuais positivos ao final de cada ano. Os fluxos de caixa em reais referentes aos finais dos anos 1, 2 e 3, respectivamente para cada projeto, são:

Projeto I: 3.060; 3.121 e 3.184

Projeto II: 2.80, 3.245 e 4.500

Projeto III: 4.080, 3.121 e 2.122

Projeto IV: 3.120, 3245 e 3.375

A uma taxa de custo de  capital (taxa de desconto) de 3% ao ano, os projetos economicamente viáveis pelo método do Valor Presente Líquido são

A) Projeto I e Projeto II

B) Projeto I e Projeto III

C) Projeto I e Projeto IV

D) Projeto II e Projeto III

E) Projeto II e Projeto IV

Resolução: Essa questão não é difícil. Ela é trabalhosa, pois temos de trazer à valor presente 12 valores, ou seja, três valores para cada um dos quatro projetos. Particularmente, durante uma prova de concurso público, eu somente faria essa questão se realmente desse tempo, apesar de ser questão de peso 2. Teríamos de pegar cada valor e trazê-lo a valor presente, usando a tabela de fator de valor presente de um pagamento único. E após isso, abatermos o valor do investimento inicial de 9.000, assim, teremos o VPL.

Calculando o VPL do Projeto I:

3.060 x FVA (3%; 1) + 3.121 x FVA (3%; 2) + 3.184 x FVA (3%; 3) =

= 3.060 x 0,9709 + 3.121 x 0,9426 + 3.184 x 0,9151 = 8.826,49;

VPL = 8.826,49 – 9.000 = (173,51)

Calculando o VPL do Projeto II:

2.080 x FVA (3%; 1) + 3.245 x FVA (3%; 2) + 4.500 x FVA (3%; 3) =

= 2.080 x 0,9709 + 3.245 x 0,9426 + 4500 x 0,9151 = 9.196,16

VPL = 9.196,16 – 9.000 = 196,16

Calculando o VPL do Projeto III:

4.080 x FVA (3%; 1) + 3.121 x FVA (3%; 2) + 2.122 x FVA (3%; 3) =

= 4.080 x 0,9709 + 3.121 x 0,9426 + 2.122 x 0,9151 = 8.844,97

VPL = 8.844,97 – 9.000 = (155,03)

Calculando o VPL do Projeto IV:

3.120 x FVA (3%; 1) + 3.245 x FVA (3%; 2) + 3.375 x FVA (3%; 3) =

= 3.120 x 0,9709 + 3.245 x 0,9426 + 3.375 x 0,9151 = 9.176,41

VPL = 9.176,41 – 9.000 = 176,41

Lembrando que para um projeto ser aceito, precisamos ter VPL positivo. Para um projeto ser rejeitado, VPL negativo. Temos, portanto, dois projetos economicamente viáveis (II e IV), e dois projetos economicamente inviáveis (I e III), segundo o método do Valor Presente Líquido. Letra E. Por incrível que pareça, na calculadora financeira HP12c chega a dar pena de resolver esse exercício, mas, eu juro, me contive, e também resolvi à mão, como, certamente, os senhores fizeram (ou tentaram).

Era isso, gente. Salvo melhor juízo, não vi questões passíveis de anulação nesta prova de matemática.

Uma boa semana a todos, e fiquem com Deus!