Vamos continuar a resolver a prova de Matemática para o Concurso Público de Assistente Legislativo da Câmara Municipal de Porto Alegre (nível médio), aplicada pela Fundatec em janeiro de 2012. Vamos às questões de Matemática de números 71 a 75. Lembrando que a prova completa do concurso de Assistente Legislativo, escaneada em pdf, deixo disponível para download por aqui: Prova Assistente Legislativo.
Somente aqui o concursando e estudante encontra provas resolvidas de concursos públicos recentes aplicados aqui no Rio Grande do Sul: vamos às próximas 5 questões!
Questão 71 – Considerando β um arco compreendido entre 0 e 2Π, qual, dentre as alternativas seguintes, apresenta uma sentença verdadeira?
A) sen (β) + cos (β) = 1
B) sen (β) – cos (β) = 1
C) sen² (4β) + cos² (4β) = 4
D) sen² (3β) + cos² (3β) = 1
E) sen² (β) + cos² (β) = 0
Resolução: Questão de trigonometria. Para quem estudou, essa foi muito fácil. Considera-se a relação trigonométrica fundamental como: sen² (x) + cos² (x) = 1, com base na relação de Pitágoras no círculo trigonométrico. Ou seja, o quadrado do seno de um arco somado com o quadrado do cosseno do mesmo arco (seja ele qual for) é sempre igual a 1. Dessa forma, a assertiva que melhor se adequa a esse princípio é a de letra D.
Questão 72 – Um aquário tem a forma de um paralelepípedo, com 40 cm de comprimento, 20 cm de largura e 30 cm de altura. Denise tem um balde de forma cilíndrica, com raio da base igual a 10 cm e altura igual a 20 cm. Para encher o aquário com ¾ de seu volume, quantos baldes cheios de água serão necessários? Considere Π = 3.
A) 1
B) 2
C) 3
D) 4
E) 5
Resolução: Questão envolvendo raciocínio quantitativo e geometria espacial. Quem estudou levemente isso aí, se deu bem nessa. O volume de um paralelepípedo é o produto de suas dimensões; ou seja: V = largura x comprimento x altura = 30 x 40 x 20 = 24.000 cm³. Precisamos, agora, calcular o volume do balde, que tem forma cilíndrica. O volume de qualquer cilindro é:
V = Π x R² x h = 3 x 10² x 20 = 6.000 cm³.
Consideremos, agora, que ¾ do volume do aquário seja de 24.000 x ¾ = 18.000 cm³. Esse valor corresponde ao volume de água que deveremos colocar no aquário. Ora, se cada balde de água possui 6.000 cm³ de água, precisaremos, então, de 3 baldes cheios para encher o aquário com ¾ de seu volume, afinal 6.000 x 3 = 18.000. Sem dúvidas, a resposta é letra C.
Questão 73 – Um presente de natal foi colocado em uma caixa com 40 cm de comprimento, 20 cm de largura e 30 cm de altura. Para embrulhar completamente essa caixa, quantos centímetros quadrados de papel, no mínimo, são necessários?
A) 4.000
B) 4.500
C) 4.800
D) 5.000
E) 5.200
Resolução: Questão envolvendo apenas geometria espacial – para não errar. Basta, nesse caso, sabermos a fórmula da área total de um paralelepípedo. Consideremos a largula L, o comprimento C, e a altura H. Teremos a seguinte fórmula para a área total (At) de qualquer paralelepípedo:
At = 2 x [ (L x C) + (L x H) + (C x H) ] = 2 x [ (40 x 20) + (40 x 30) + (30 x 20) ]
Assim, At = 2 x [ (800) + (1.200) + (600) ] = 2 x [ 2.600 ] = 5.200. Letra E.
Questão 74 – Sabe-se que o valor máximo atingido por uma função do segundo grau, cuja concavidade está voltada pra baixo, é a ordenada do seu vértice. Então dada a função:
f (x) = 4 (-x – 5) (x – 45)
que representa, em milhares de reais, o lucro de produção de x unidades (x em centenas) de certo produto, qual será o lucro máximo (em milhares de reais) de produção desse produto?
A) 1.800
B) 2.000
C) 2.500
D) 3.200
E) 4.000
Resolução: Questão envolvendo função do segundo grau. No próprio início da questão, o examinador já dá a seguinte dica: o valor máximo atingido por uma função do segundo grau, cuja concavidade está voltada pra baixo, é a ordenada do seu vértice. Só faltava mesmo ele dar a fórmula das coordenadas do vértice.
Bom, o primeiro passo para solucionarmos esse problema é desenvolvermo a equação do 2° grau, que está na forma reduzida f (x) = 4 (-x – 5) (x – 45). Fazendo esse desenvolvimento e o adequado produto entre os dois binômios teremos:
f (x) = -4x² + 160x +900.
É necessária essa forma desenvolvida, pois, agora, sabemos os valores de A, B e C, coeficientes dos termos de qualquer função desse tipo. Portanto A = -4, B = 160, e C = 900.
Agora, podemos calcular o valor do vértice em X e, pegando esse valor, substituímos na função principal desenvolvida. Achei mais fácil de fazer desse modo. O valor do vértice em X, é dado pela seguinte fórmula:
Vx = -B/2A = -160/-8 = 20.
Sabemos, então, que o valor máximo que a função atinge é quando o valor de x é de 20. Substituímos 20 em f (x) = 4 (-x – 5) (x – 45).
Ora, f (20) = 4 (-25) (-25) = 2.500.
Poderíamos, de outra forma, ter calculado direto o vértice em Y, mas precisaríamos saber o valor do discriminante
Δ (delta) = B² – 4AC = 40.000.
Assim, pegaríamos a fórmula do vértice em Y:
Vy = -Δ/4A = -40.000/-16 = 2.500.
Eu faria da primeira maneira, para não ter que calcular Δ, mas isso vai de cada um. Resposta certa: letra C.
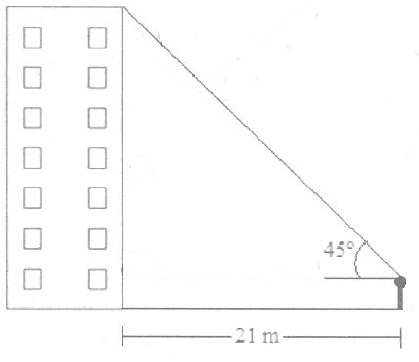
Questão 75 – Uma pessoa com 170 cm de altura avista o topo de um prédio a uma distância de 21 m deste, sob um ângulo de 45°, conforme mostra a figura a seguir.
.
.
Nessas condições, a altura do prédio é igual a
A) 21,0 m
B) 22,7 m
C) 24,0 m
D) 25,7 m
E) 26,0 m
Resolução: Lembro que quando começamos a estudar trigonometria no colégio, os primeiros tipos de exercícios que resolvemos são desse tipo. Um triângulo retângulo, um ângulo dado, uma medida de algum lado, e manda calcular os outros. Essa questão não foge disso. A questão saideira deste post é a mais fácil de todas. Pede a altura do prédio que corresponde ao cateto oposto ao ângulo dado. A questão dá também a medida do cateto adjacente ao ângulo dado, que é de 21 cm. Ora, se temos um ângulo e temos a medida do cateto adjacente, podemos facilmente calcular a medida do cateto oposto pela fórmula da tangente, que é tg α = cateto oposto / cateto adjacente. Ocorre que nos é dado a medida do ângulo α, que é de 45°. Ora, a tg 45° = 1, por definição. Seja X a medida do cateto oposto; temos que: tg 45° = X/21. Portanto, resolvendo, teremos X = 21. Não esqueçamos de adicionar a esse valor a altura do observador, portanto, ficando a altura total do prédio em 21 + 1,70 = 22,70 m. Não dê uma de concurseiro novato, caindo na pegadinha de marcar letra A… A resposta correta está logo depois: letra B.
Essa terceira bateria de 5 questões foram mais fáceis de serem resolvidas. O problema mesmo é o tempo. Eu, por exemplo, estou aqui em uma sala com ar condicionado tranquilamente sentado com livros à minha volta, um suco de laranja e um pedaço de bolo para me distrair. Na hora de uma prova de concurso, o ambiente é muitas vezes hostil, com fiscais de olho em ti, te acompanhando no banheiro, no máximo, pode-se tomar uma água morna em salas quentes sem ventilação com bancos duros… E apesar de tudo isso, o cara tem ainda que ter raciocínio rápido na hora da prova e não babar em questões fáceis como essas. Reconheço pois já passei por isso: é buxa!
Quaisquer dúvidas ou comentários ou sugestões de provas e exercícios, escrevam abaixo, que assim que puder, eu certamente responderei!
Espero, no próximo post, finalmente encerrar essa prova de 20 questões de Matemática da Fundatec. Até lá.
Aguardem e estudem!