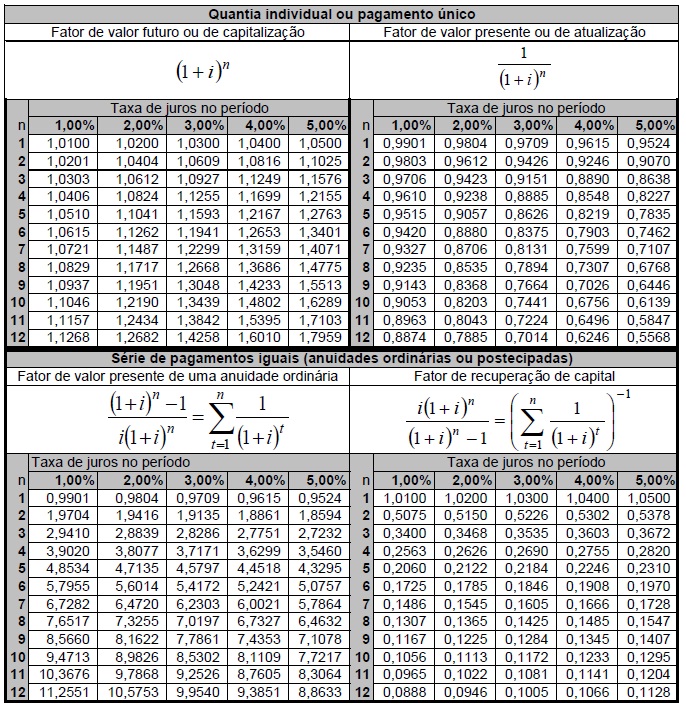
Resolvo aqui a prova de Matemática Financeira, aplicada pela da FMP (Fundação do Ministério Público/RS), para o Cargo de Agente Público Externo do TCE-RS – Área Administração (2011). A parte da prova envolvendo Matemática Financeira contemplava apenas 5 questões. Provas desse tipo, eu aconselho ao concursando treinar muito cálculos de números com vírgulas, envolvendo soma, subtração, divisão e multiplicação. A prova disponibilizava também a tabela financeira abaixo para facilitar os cálculos, que deviam ser feitos “no braço”:
Vamos então à prova:
66 – O rendimento de R$ 1.500,00 aplicados por três meses à taxa de juros simples de 30% ao ano é:
(A) R$ 112,50.
(B) R$ 1.612,50.
(C) R$ 1.800,00.
(D) R$ 3.784,15.
(E) R$ 4.284,15.
Resolução:
Questão bem comum de juros simples. A taxa está na forma anual e o prazo está em meses. Como a aplicação é feita por juros simples, a taxa é proporcional, ou seja, podemos tranformar a taxa anual para mensal simplesmente dividindo o seu valor por 12, afinal, existem 12 meses dentro de um ano. Fazendo essa divisão de 30/12, teremos uma taxa mensal de 2,5%. Aplicando a fórmula dos juros:
J = C x i x n = 1.500 x 0,025 x 3 = 112,50 (letra a). Lembrando que a questão pede o rendimento, ou seja, os juros gerados pela aplicação. Se pedisse o montante, ou valor acumulado, a resposta seria a letra b.
67 – A aplicação de R$ 22.000,00 em um fundo que rende juros compostos à taxa de 2% ao mês acumula um saldo após o sétimo mês de:
(A) R$ 3.080,00.
(B) R$ 3.271,40.
(C) R$ 25.080,00.
(D) R$ 25.271,40.
(E) R$ 27.900,40.
Resolução:
Questão fácil envolvendo juros compostos. A questão pede o montante desta aplicação. A fórmula do montante em juros compostos é uma fórmula exponencial: M = C x (1 + i)^n. Ou seja, multiplicamos o valor do capital pelo fator de valor futuro ou capitalização (1 + i)^n. Esse valor está disponível na primeira tabela, olhando na linha 7, coluna 2 desta tabela veremos o valor de 1,1487, que é o fator de capitalização. Multiplicando-se esse fator por 22.000, que é o valor da aplicação, teremos 25.271,40, que é o montante, ou valor acumulado da aplicação (letra d).
68 – A taxa efetiva anual equivalente à taxa nominal de 18% ao semestre capitalizados mensalmente é:
(A) 15,08%.
(B) 21,49%.
(C) 25,66%.
(D) 19,41%.
(E) 42,58%.
Resolução:
Nessa questão, primeiro devemos transformar a taxa, que está na forma nominal, pois o período da taxa (semestral) é distinto do períodos da capitalização (mensal). Sempre uma taxa na forma nominal deve ser transformada, antes de tudo, para a sua efetiva respectiva. Então vamos fazer a seguinte divisão: 18/6, afinal, existem seis capitalizações mensais em um período semestral. Teremos agora uma taxa efetiva mensal de 3%. Agora devemos transformar essa taxa efetiva mensal para efetiva anual, bastando para isso irmos na mesma tabela de antes, procurando a linha 12 e a coluna 3, e acharemos o fator de 1,4258. Abatemos um deste valor e teremos 0,4258, ou em percentual 42,58% (letra e). Se em juros simples a taxa seria 3 x 12 = 36% a.m. é óbvio que em juros compostos a taxa equivalente ficará acima desse valor, nem precisando procurar em tabela nenhuma, afinal, a única alternativa disponível acima de 36% seria o gabarito e.
69 – Um a pessoa faz aplicações mensais iguais a R$ 2.000,00 num fundo que remunera à taxa de juros compostos de 1% ao mês. Após a décima aplicação o saldo do fundo é:
(A) R$ 18.942,60.
(B) R$ 20.000,00.
(C) R$ 20.924,00.
(D) R$ 21.120,00.
(E) R$ 22.092,00.
Resolução:
Questão envolvendo séries de pagamentos. Nessa, o examinador pede o saldo acumulado de aplicações uniformes e sucessivas de 2.000, à taxa de 1%, durante 10 meses. Como não é disponibilizada a tabela do fator de acumulação de capital de uma série de pagamentos, a saída será calcularmos primeiro o valor presente da série e depois fazermos a capitalização desse valor em 10 períodos. Pegamos a tabela do fator de valor presente na linha 10, coluna 1, e vemos o valor de 9,4713. Esse valor, multiplicamos por 2.000. Teremos então 18.942,60. Agora capitalizamos esse valor único em juros compostos, durante 10 meses à taxa mensal de 1%. Vamos novamente na primeira tabela, agora na linha 10, coluna 1, e pegamos o valor de 1,1046 e multiplicamos esse fator por 18.942,60, que é o valor presente calculado antes. Teremos a resposta do gabarito c, ou seja, 20.924. Nesta questão, tivemos de nos adaptar às tabelas fornecidas. Mais fácil seria pegar logo a tabela da FAC, mas como não foi disponibilizada na prova, devemos nos adaptar com as outras.
70 – Uma empresa obtém um empréstimo de R$ 12.000,00, num banco de desenvolvimento o financiamento, cuja taxa efetiva de juros compostos é de 2% ao mês. A empresa deseja amortizar a dívida em doze meses, sabendo-se que, em todos os planos o primeiro pagamento é após trinta dias do financiamento. O banco de desenvolvimento oferece os seguintes planos de amortização: Pagamento Periódico de Juros, Sistema Price e Sistema de Amortizações Constantes (SAC). Os últimos pagamentos de cada plano, respectivamente, são:
(A) R$ 240,00; R$ 1.135,20; R$ 1.020,00.
(B) R$ 240,00; R$ 1.268,20; R$ R$ 1.135,20.
(C) R$ 12.240,00; R$ 1.135,20; R$ 1.268,00.
(D) R$ 1.268,20; R$ 12.240,00; R$ 1.020,00.
(E) R$ 1.135,20; R$ 1.020,00; R$ 240,00.
Resolução:
Última questão envolvendo sistemas de amortização. A primeira forma envolve o pagamento periódico de juros, ou simplesmente Sistema Americano. Nesse sistema, paga-se somente os juros durante o prazo do empréstimo. No final, paga-se os juros juntamente com o principal. No caso, teremos juros de 2% sobre 12.000, que é 240. Como pede o último pagamento desse plano, o total será 12.000 + 240 = 12.240.
Mas vamos adiante. No Sistema Price, todas as prestações são iguais, tanto a primeira quanto a última. Basta pegarmos o valor do empréstimo e multiplicarmos pelo fator de recuperação de capital, disponível na última tabela, linha 12, coluna 2, e teremos o fator 0,0946. Esse valor multiplicado pelo principal nos dará a prestação: 1.135,20.
Para finalizar, vamos na tabela SAC. Nesse sistema, as amortizações são constantes durante todo o prazo do empréstimo. O valor da amortização fica em 12.000/12, que será de 1.000. Ou seja, todo o mês, é amortizado do saldo devedor o valor de 1.000. Lembrando que Prestação = juros + amortização. Amortizar significa abater efetivamente da dívida, certo? No último período, falta amortizar somente uma parcela. Portanto, o saldo devedor antes de pagar a última prestação será de 1.000. Aplicamos 2% sobre esse saldo e teremos os juros pagos na última prestação, ou seja, 1.000 x 0,02 = 20. Somando agora 20 + 1.000 = 1.020, que será o valor da ultima prestação pelo sistema de amortização constante. O gabarito não contempla essa sequência de resposta, razão pela qual a questão foi anulada.
Deixo um abraço a todos, e espero ter ajudado!