Um assunto raramente tratado nas faculdades e nos melhores livros e apostilas de finanças vai ser tópico descrito minuciosamente AQUI no blog: o sistema de capitalização contínua em Matemática Financeira.
Introdução
Desde que ministro aulas particulares de matemática financeira para concursos, seja online ou presencial, é rara a cobrança desse conteúdo; muito embora, nos últimos anos, tenho percebido que bancas como a Cespe, a FCC e a FGV vêm cobrando questões envolvendo juros contínuos.
Prefere em vídeo?
O conteúdo deste post também está disponível em formato de vídeo! Aproveite e se inscreva no meu canal aprendamatematica no youtube! Ali procuro comentar assuntos interessantes, como este aqui do blog, envolvendo matemática, estatística, contabilidade, pesquisa operacional, editais e concursos públicos.
Finalidade e utilidade
Antes de tudo, a capitalização contínua é um conceito fundamental que é usado para calcular juros compostos em investimentos de longo prazo e permite que os juros sejam calculados instantaneamente ao longo do tempo, em vez de serem calculados em intervalos fixos – normalmente em finais de períodos.
Como acima escrevi, sua utilidade se foca em investimentos de longo prazo: como fundos de aposentadoria, pois permite que os juros compostos sejam calculados com mais realidade e precisão. Em vez de calcular os juros apenas uma vez por ano ou a cada seis meses, a capitalização contínua calcula os juros a cada instante. Isso significa que, no longo prazo, o investimento cresce mais rapidamente do que se os juros fossem apenas calculados em intervalos estanques de tempo.
Veja bem. Embora a capitalização contínua possa parecer complexa, é um conceito importante que vale a pena entender. Se você planeja fazer algum tipo de investimento de longo prazo, é salutar entender o funcionamento a fundo dos juros compostos e também como a capitalização contínua pode afetar seu valor futuro.
Conceitos de capitalização simples, composta e contínua
No estudo da Matemática Financeira existem três regimes de capitalização: simples, composto e contínuo. Cada uma dessas formas de capitalização possui suas próprias características e fórmulas.
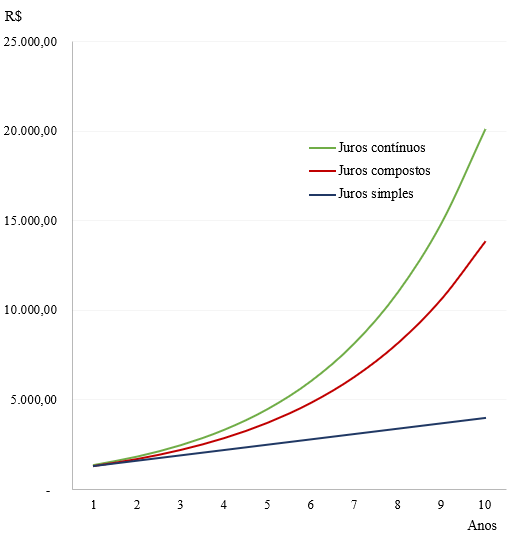
No gráfico acima, observamos a sobreposição dos gráficos de cada um dos três regimes de capitalização. Nota-se em juros simples um crescimento linear do montante (linha azul). Já no juro composto, ocorre o efeito da capitalização dos juros sobre juros, tornando a função exponencial (linha vermelha). E por fim, temos o gráfico da capitalização contínua (linha verde), com crescimento exponencial superior ao juro composto.
No juro simples temos o método mais básico de capitalização. Nele os juros são calculados tão-somente sobre o capital inicial. Ou seja, o valor dos juros permanece constante ao longo do tempo, já que é mantida uma taxa constante sobre um capital constante, independentemente do tempo de aplicação do capital.
Por outro lado, na capitalização composta, os juros são calculados sobre o capital inicial e também sobre os juros acumulados. Isso significa que, ao longo do tempo, o valor dos juros aumenta exponencialmente, tornando a capitalização composta mais vantajosa, para quem aplica, do que a capitalização simples.
Por sua vez, a capitalização contínua é um método ainda mais avançado de capitalização. Nesse caso, os juros são calculados de forma contínua, ou seja, a cada instante de tempo. Dessa forma, a taxa de juros é aplicada de forma infinitesimal, o que resulta em uma maior precisão nos cálculos.
Muito embora a capitalização contínua seja a forma mais precisa de capitalização, ela é a menos utilizada na prática, devido à sua complexidade matemática e à dificuldade de implementação em sistemas financeiros.
Definição de taxas nominais e efetivas em juros compostos
Quando se trata de juros compostos, é importante entender a diferença entre as taxas nominais e efetivas. A taxa nominal é a taxa de juros que é declarada pelo credor ou instituição financeira. Já a taxa efetiva é a taxa real de juros que é paga pelo tomador do empréstimo ou investidor; normalmente essa é superior àquela declarada em contrato.
Para melhor compreensão, suponhamos um investimento de R$ 1.000,00 remunerado a uma taxa nominal de 12% ao ano, com capitalização mensal. Isso significa que em um ano ocorrerão 12 capitalizações mensais, de forma acumulada, juros sobre juros. Em cada capitalização mensal, teremos juros compostos de 1% ao mês (12/12).
Ok, mas se considerarmos a taxa efetiva anual, que é a taxa real de juros que o investidor receberá no ano todo, podemos calculá-la da seguinte forma:
- 1 + i = (1 + 0,12/12)^12
- 1 + i = (1,01)^12
- i = 1,1268 – 1 = 0,1268 ou, em forma percentual, 12,68% ao ano/ano (taxa efetiva anual).
Isso significa que a taxa anual efetiva de juros que o investidor receberá é de 12,68%, e não 12%, como inicialmente parece indicar em sua forma nominal.
É importante lembrar que quanto maior a frequência de capitalizações em determinado período, maior será a diferença entre a taxa nominal e a taxa efetiva. A taxa nominal é uma taxa aparente: ela parece, mas não é. Parece cobrar 12% ao ano, mas na verdade cobra 12,68% anuais e efetivos – tudo por causa do efeito das capitalizações mensais.
Portanto, ao calcular os juros compostos em um investimento ou empréstimo, é essencial levar SEMPRE em consideração a taxa efetiva, que representa a taxa real de juros que deve ser implementada no cálculo.
Assim, quanto mais capitalizações, maior será a taxa efetiva equivalente. Uma capitalização horária, por exemplo, trará um efeito ainda superior aos 12,68%? E se a capitalização fosse por segundos? Ou por décimos ou centésimos de segundos? Por fim, se a capitalização fosse infinita, quase que instantânea, o que aconteceria?
Juros compostos e o número de Euler
Os juros compostos são um dos conceitos mais importantes em Matemática Financeira, pois eles são amplamente utilizados no mercado financeiro brasileiro. Veja bem que eles se referem ao cálculo dos juros sobre um valor inicial que inclui não apenas o principal, mas também os juros acumulados. Muito bem!
O número de Euler, representado pela letra “e”, é um número irracional que aparece em muitas áreas da matemática, incluindo a matemática financeira. Ele é definido como a base dos logaritmos naturais e tem um valor aproximado de 2,71828.
Quando se trata de juros compostos, o número de Euler é importante, pois ele é usado para calcular a taxa de juros contínua. A taxa de juros contínua é a taxa de juros que seria necessária para produzir o mesmo resultado dos juros compostos em um período de tempo específico.
A fórmula para calcular a taxa de juros contínua é:
r = ln(1 + i)
Onde “r” é a taxa de juros contínua (ou taxa instantânea) e “i” é a taxa de juros efetiva.
Usando essa fórmula, podemos encontrar a taxa de juros contínua para qualquer período de tempo.
Por exemplo, se a taxa de juros efetiva for de 6% ao ano, a taxa de juros contínua seria de aproximadamente 5,96% ao ano.
Em resumo, o número de Euler é uma ferramenta importante em matemática financeira porque nos permite calcular a taxa de juros contínua, que é essencial para se entender como os juros compostos funcionam em períodos de capitalizações ínfimas de tempo, quase tendentes a zero.
Fórmula da capitalização contínua
A fórmula da capitalização contínua é utilizada para calcular o valor futuro de um investimento que está sendo continuamente capitalizado. Ela é expressa da seguinte forma:
M = C x ert
Onde:
- M é o montante ou valor futuro do investimento
- C é o capital inicial ou valor presente do investimento
- “e” é a constante de Euler (aproximadamente 2,71828)
- r é a taxa de juros instantânea
- t é o período da aplicação
A propósito, se quiser saber melhor como se chega a essa fórmula, sua dedução está detalhadamente explicada no vídeo em meu canal aprendamatemática, no youtube – acima compartilhado neste post.
A fórmula da capitalização contínua é especialmente útil para investimentos que têm um tempo de vida longo e não têm um período definido de capitalização.
Por exemplo, se um investimento é continuamente capitalizado a uma taxa de juros de 5% ao ano, a fórmula pode ser usada para calcular o valor futuro do investimento após 10 anos.
É importante notar que a fórmula da capitalização contínua assume que a taxa de juros permanece constante durante todo o período de investimento. Se a taxa de juros variar ao longo do tempo, a fórmula precisa ser ajustada para levar em conta essas mudanças. Além disso, a fórmula da capitalização contínua é baseada em juros compostos, o que significa que os juros são calculados não apenas sobre o valor inicial do investimento, mas também sobre os juros acumulados. Isso significa que o montante da aplicação aumenta exponencialmente ao longo do tempo, o que pode levar a grandes retornos no longo prazo.
Fórmula da taxa instantânea e da taxa efetiva
Na capitalização contínua, a taxa de juros é considerada como uma taxa instantânea, ou seja, uma taxa que é calculada para um intervalo de tempo infinitamente pequeno.
A fórmula para calcular a taxa instantânea é dada por:
r = ln(1 + i)
Onde:
- r é a taxa instantânea
- i é a taxa de juros efetiva
- ln é o logaritmo natural ou neperiano, ou seja, que usa como base a constante de Euler.
Assim, usando álgebra de logaritmos e isolando i, teremos a fórmula da taxa efetiva, que é a taxa de juros que leva em consideração o efeito real da capitalização. A fórmula para calcular a taxa efetiva é dada por:
i = er – 1
Onde:
- i é a taxa efetiva
- r é a taxa instantânea
- “e” é a constante de Euler
Exemplos de Aplicação
Exemplo 1
Suponha que eu queira investir R$ 10.000,00 em uma aplicação financeira que rende 1,5% anual. Se eu optar pela capitalização anual, qual será o montante acumulado após 2 anos?
| Ano | Saldo Inicial | Juros | Saldo Final |
| 1 | R$ 10.000,00 | R$ 150,00 | R$ 10.150,00 |
| 2 | R$ 10.150,00 | R$ 152,25 | R$ 10.302,25 |
Após 2 anos, o montante acumulado será de R$ 10.302,25.
Exemplo 2
Suponha agora o mesmo investimento do exemplo anterior, agora usando capitalização contínua.
Usando a fórmula da capitalização contínua, temos:
M = C x (e^(r*t)) = 10.000 x 1,0300454534 = 10.304,54, superior aos 10.302,25 anteriormente apurados.
Exemplo 3
Calcule o montante de uma aplicação de R$ 1.000,00, com taxa de 12% ao ano, capitalizada continuamente, durante 1 ano:
M = C x (e^(r*t)) = 1.000 x e^(0,12 x 1) = 1.000 x 1,127496 = R$ 1.127,50
Exemplo 4
Calcule o valor futuro de uma aplicação de R$ 1.000,00, com taxa mensal instantânea de 3%, durante 5 meses, com capitalização contínua.
M = C x (e^(r*t)) = 1.000 x e^(0,03 x 5) = 1.000 x 1,161834 = R$ 1.161,83
Exemplo 5
Calcule o valor de uma aplicação com valor futuro de R$ 1.000,00 ao final de 8 meses, considerando uma taxa mensal de 5%, com capitalização contínua.
Usando a fórmula dessa vez para o valor presente da capitalização contínua, temos:
PV = FV / (e^(r*t)) = 1.000 / e^(0,05 x 8) = 1.000 x 1,491824 = R$ 670,32
Exemplo 6
Apliquei o valor de R$ 2.400,00 e, ao fim de 9 meses, saquei o total de R$ 3.000,00; considerando o uso de capitalização contínua, calcule as taxas instantânea e efetiva na operação:
Apenas passamos o PV como denominador de FV, na fórmula, a fim de calcularmos a taxa instantânea:
FV/PV = (e^(r*t))
3.000 / 2.400 = e^(9 x r)
1,25 = e^(9 x r), agora precisamos a partir da igualdade calcularmos ln (logaritmo natural) em cada lado da igualdade:
ln 1,25 = ln e^(9 x r)
0,223143 = (9 x r) x ln e
0,223143 = (9 x r) x 1, logo temos… r = 0,223143 / 9 = 0,0248 = 0,0248 x 100 = 2,48% ao mês
E agora, vamos ao cálculo da taxa efetiva na operação:
i = e^r – 1 = e^0,0248 – 1 = 1,0251036 – 1 = 0,0251036 = 0,0251036 x 100 = 2,51% ao mês
Poderíamos, para o cálculo da taxa efetiva mensal em juros compostos usar os seguintes passos na calculadora financeira HP12c – pra quem não tem a calculadora HP12c, superindico o acesso a esse link de uma calculadora financeira online: acesse aqui.
3000 FV
2400 CHS PV
9 n
i …. 2,51% ao mês
Questões resolvidas e explicadas?
No meu canal “aprendamatematica” (Youtube) filmei um resumo sobre capitalização contínua com resolução detalhada de 13 questões de concursos públicos recentes das principais bancas do país, tais como FCC, Cespe, dentre outras. Acesse abaixo: aproveite e se inscreva no canal!
Vantagens e desvantagens da capitalização contínua
Vantagens
Uma das principais vantagens da capitalização contínua é que ela permite uma maior precisão nos cálculos financeiros. Ao invés de utilizar um período de tempo fixo, como acontece na capitalização simples e composta, a capitalização contínua utiliza um tempo infinitesimalmente pequeno, o que resulta em valores mais precisos.
Outra vantagem é que a capitalização contínua é capaz de gerar (para quem aplica) maiores rendimentos em investimentos de longo prazo. Isso ocorre porque, quanto maior o tempo de investimento, maior será a diferença entre a capitalização contínua e as outras formas de capitalização.
Desvantagens
Uma das principais desvantagens da capitalização contínua é que ela é mais complexa do que as outras formas de capitalização. Isso pode tornar os cálculos mais difíceis e aumentar o risco de erros.
Além disso, a capitalização contínua pode não ser adequada para todos os tipos de investimentos. Por exemplo, em investimentos de curto prazo, os ganhos com a capitalização contínua podem ser insignificantes em comparação com as outras formas de capitalização.
Aplicações da capitalização contínua
A capitalização contínua é muito utilizada em diversas áreas da matemática financeira. Abaixo estão algumas aplicações práticas da capitalização contínua:
- Cálculo de juros compostos: a capitalização contínua é uma forma de calcular juros compostos de forma mais precisa e eficiente do que a capitalização periódica.
- Modelagem de processos estocásticos: a capitalização contínua é utilizada para modelar processos estocásticos em finanças e outras áreas, como física e biologia.
- Cálculo de derivativos financeiros: a capitalização contínua é utilizada no cálculo de derivativos financeiros, como opções e futuros.
- Cálculo de taxas de juros: a capitalização contínua é utilizada para calcular taxas de juros em empréstimos, investimentos e outros tipos de transações financeiras no longo prazo.
Além disso, a capitalização contínua é amplamente utilizada em diversos modelos matemáticos, como o modelo Black-Scholes para opções financeiras e o modelo de Merton para default de empresas (moratória).
Assim sendo, a capitalização contínua é uma ferramenta poderosa e versátil da Matemática Financeira, que é amplamente utilizada em diversas áreas e aplicações práticas.
Conclusão
Após a análise detalhada da capitalização contínua em matemática financeira, posso afirmar que essa técnica é uma ferramenta valiosa para calcular juros compostos em situações em que o tempo é contínuo. A fórmula de capitalização contínua é simples e fácil de usar, mas é importante lembrar que ela só é aplicável em situações em que o tempo é medido em unidades contínuas.
Além disso, a capitalização contínua também pode ser usada para calcular o valor presente de um fluxo de caixa contínuo, o que pode ser útil em muitos contextos financeiros. No entanto, é importante lembrar que a capitalização contínua não é a única técnica disponível para calcular juros compostos, e em algumas situações, outras técnicas podem ser mais adequadas.
Em resumo, a capitalização contínua é uma técnica valiosa para calcular juros compostos em situações em que o tempo é contínuo. No entanto, é importante ter em mente suas limitações e considerar outras técnicas disponíveis quando necessário.
Se você chegou até aqui na leitura, parabéns! De modo algum o assunto aqui se esgota, mas espero ter contribuído positivamente em relação a essa forma de capitalização tão pouco tratada nos livros e na academia.
Se você for concurseiro, ou mesmo se não seja, mas pretenda no futuro se preparar, acesse uma interessante prova completa de matemática financeira, toda resolvida aqui por mim, para o concurso público para o cargo de Auditor da CAGE/RS, ano 2014.
Caso interesse houver, também presto assessorias financeiras para viabilidade de projetos de investimentos e financiamentos pessoais e para empresas; além de ministrar aulas particulares online de matemática financeira para concursos e faculdades.
Contate-me pelo email alexandrecorreaprof@gmail.com, ou se preferir, diretamente pelo fone/whats (51) 998172943. Um abraço a todos e fiquem com Deus!
