Umas das principais funções que estudamos desde o ensino fundamental e médio (até o ensino superior para alguns), é a função do 1° grau, também conhecida como função afim. Essa função é também estudada em diversas disciplinas de Cálculo e Estatística em Cursos de Graduação. Na verdade, no estudo do Cálculo ela é fundamental, uma vez que para se saber a equação de uma reta tangente a uma curva em um dado ponto, precisamos saber as bases de sua formação.
Desde comecei a dar aulas particulares de Cálculo em Porto Alegre, notei que a dificuldade dos alunos residem, muitas vezes, em conceitos básicos. A compreensão do comportamento de uma função afim é indispensável para se ter sucesso em cadeiras de Cálculo, que invariavelmente costumam reprovar muitos calouros.
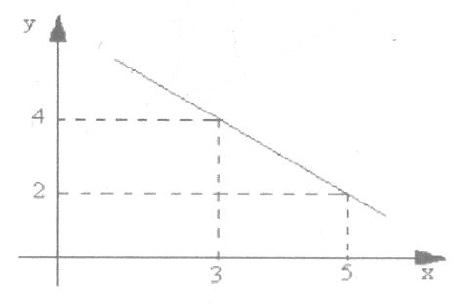
Inicialmente, vamos observar um gráfico qualquer de uma função afim:
.
.
.
.
.
.
Notamos que, antes de tudo, o gráfico da função afim é sempre representado por uma reta. E essa reta necessariamente deve ser crescente ou decrescente. A função ao lado demonstra uma função afim decrescente, pois, à medida que avançamos no eixo X, observamos que a função descresce em Y. Se a função não for crescente nem descrescente, ela não é função afim, mas, sim, função constante, que não será o foco de nossa análise aqui.
Toda e qualquer função afim tem por expressão algébrica a seguinte forma:
Y = AX + B;
Onde:
A: é o coeficiente angular da reta, também denominado declividade ou inclinação, se A>0, temos inclinação positiva ou crescente; se A<0, temos inclinação negativa, ou descrescente. Essa inclinação pode ser obtida de diversas formas:
– pela razão entre a variação de y e a variação de x: Δy/Δx, onde Δy = Y2 – Y1; e Δx = X2 – X1;
– ou pela derivada da reta tangente a uma curva em determinado ponto.
B: é o coeficiente linear da reta, ou intercepto em Y, ou seja, corresponde à intersecção da reta com o eixo Y. Na reta acima, notamos que esse coeficiente será algum valor acima de 4, pois notamos que a reta cruza o eixo Y em algum valor acima de 4. Também podemos chamar de termo independente da expressão, isto é, é o valor que independe do valor assumido por X na equação da reta. Assim, quando X for nulo, teremos o cruzamento da reta em Y.
Na função acima, temos informados dois pontos: (3, 4) e (5, 2); portanto Δy = 2 – 4 = -2; e Δx = 5 – 3 = 2; assim, temos Δy/Δx = -2/2 = -1; ou seja A=Δy/Δx = -2/2 = -1. Falta-nos agora o valor de B (coeficiente linear).
Temos como forma genérica de uma reta a seguinte função: Y = AX + B. Substituindo A por -1, e X e Y, escolhemos um dos dois pontos dados. Escolho (3, 4), assim: X = 3 e Y = 4.
Então, temos: 4 = -1 . 3 + B, isolando B, temos: B = 4 + 3 = 7, logo o coeficiente linear será igual a 7, ou seja, a reta cruzou o eixo das ordenadas em 7; e a função que representa a reta acima é: Y = – X + 7.
Sabendo disso, podemos calcular o zero da função, ou raiz da função afim. A raiz, ou zero de uma função, é o valor de X que anula a função, ou seja, a função fica zerada. Dessa forma, devemos ter: Y = 0; ou -X +7 = o, logo X = 7.
Isso significa que a função cruzará o eixo das abscissas em 7, ou no ponto (7, 0). Como a função acima é descrescente, ela passa de positiva para negativa a partir desse ponto.
Bom, era isso. Deixo forte abraço a todos os visitantes do site e até a próxima!